Pravidelné mnohouholníky v tvorbe výplní
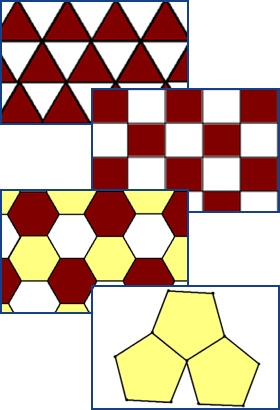
Uvažujme o vyplňovaní roviny pravidelnými mnohouholníkmi. Je zrejmé, že súčet veľkostí vnútorných uhlov mnohouholníkov zoskupených pri každom vrchole pravidelného mnohouholníka musí byť 360°.
Ktoré pravidelné mnohouholníky môžu byť použité pri tvorbe výplní?
|
|||
|
|||
|
Pre tvorbu vlastných výplní sa odporúča využiť sieť tvorenú z niektorých vyššie uvedených pravidelných n-uholníkov. Postup tvorby výplní si môže čitateľ naštudovať z odporúčanej literatúry.