Čo sú konvexné pravidelné mnohosteny?

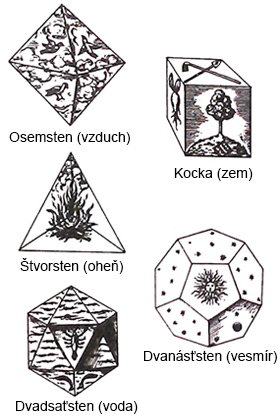
Platónova atomická teória hmoty na ilustráciách
Johannesa Keplera
Konvexné pravidelné mnohosteny sú telesá, pre ktoré platí, že všetky steny sú zhodné pravidelné mnohouholníky a každý vrchol telesa je incidentný s konštantným počtom hrán alebo stien.
V trojrozmernom Euklidovskom priestore existuje práve päť typov pravidelných mnohostenov:
  • 1.
    pravidelný štvorsten – steny tvoria rovnostranné trojuholníky,
  • 2.
    pravidelný šesťsten (kocka) – steny tvoria štvorce,
  • 3.
    pravidelný osemsten – steny tvoria rovnostranné trojuholníky,
  • 4.
    pravidelný dvanásťsten – steny sú tvorené pravidelnými päťuholníkmi,
  • 5.
    pravidelný dvadsaťsten – stenami sú opäť rovnostranné trojuholníky.
Konvexné pravidelné mnohosteny sú známe aj pod názvom Platónovské telesá. Platón síce nebol ich objaviteľom, ale podrobne študoval ich vlastnosti. Každé teleso považoval za predstaviteľa jedného zo štyroch živlov: zem, vzduch, voda a oheň, pričom dvanásťsten bol predstaviteľom všetkého, čo existuje, najmä z dôvodu jeho ťažkej geometrickej konštrukcie (využitie zlatého rezu). Matematický opis Platónovských telies predložil Euklid vo svojich Základoch. Našiel pomer priemeru opísanej kružnice a dĺžky hrany príslušného telesa a uviedol, že pravidelných mnohostenov je práve päť typov.