Vzdialenosť bodu od lineárneho podpriestoru
Vzťah pre výpočet vzdialenosti bodu od lineárneho podpriestoru je dôsledkom vzťahu z vety 8L3, a to:
| Nech pre A ľubovoľný bod A a bod A* ∈ α platí, že vektor A* - A je kolmý na podpriestor α. Potom |Aα| = |AA*|. |
Vzdialenosť bodu od priamky možno vypočítať buď podľa vety 8L2 ako vzdialenosť bodu od jeho kolmého priemetu do lineárneho podpriestoru (
obr. 8L3a
), alebo podľa dôsledku vety 8L3 ako dĺžku vektora, ktorý:
|
|||
|
|||
|
Na výpočet vzdialenosti bodu od nadroviny v priestore E
n
danej všeobecnou rovnicou, špeciálne na výpočet vzdialenosti bodu od priamky (nadroviny) v E
2 a vzdialenosti bodu od roviny (nadroviny) v E
3 sa používa vzorec opísaný v nasledujúcej vete:
|
Veta 8L4. Nech v priestore E
n
je daný bod a nadrovina α: a
1
x
1 + a
2
x
2 + … + a
n
x
n
+ a
0 = 0. Potom |Aα| = |a 1 x 1 0 + a 2 x 2 0 + … + a n x 0 0 + a 0| / 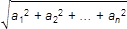 .
. |
Ak poznáme normálový vektor nadroviny a bod, ktorým prechádza nadrovina, možno vzdialenosť bodu od nadroviny vypočítať podľa vzorca v nasledujúcom dôsledku:
| Pre vzdialenosť bodu A od nadroviny α: n.(X - P) = 0 platí |Aα| = |n.(A-P)| / |n| Pre výpočet vzdialenosti bodu od priamky v E 2 a bodu od roviny v E 3 stačí vo vzorci z vety 8L4 položiť n = 2 resp. n = 3 (
obr. 8L4a
,
8L4b
). |