Uhol dvoch priamok
Základné vlastnosti uhla dvoch priamok možno zhrnúť v nasledujúcej vete:
|
Veta 9L2. Nech a, b sú dve priamky euklidovského priestoru E
n
so smerovými vektormi a, b. Potom: a) ∠ab priamok a, b je číslo φ ∈ <0, π/2>, b) ∠ab = 0 ⇔ a || b, c) ∠ab = π/2 ⇔ a | b. |

Poznámka 9L5.
Uhol priamok daných parametricky vypočítame podľa vzorca z nasledujúcej vety:
|
Veta 9L3. Nech a = A + <a>, b = A + <b>, kde a = (a
1, a
2, …, a
n
), b = (b
1, b
2, …, b
n
). Potom pre uhol φ priamok a, b v priestore E
n
platí: cos φ = |a 1 b 1 + a 2 b 2 +…+ a n b n | / 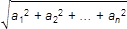 .
.
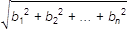 .
. |