Násobenie a lineárna kombinácia vektorov
|
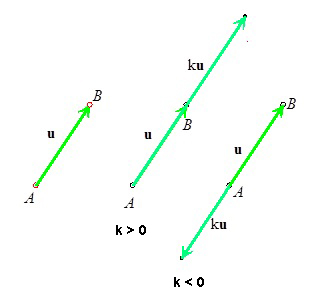
Definícia 1L4. Nech r je reálne číslo rôzne od nuly (t. j. r ≠ 0). Násobkom nenulového vektora u = B - A číslom k sa nazýva vektor r ∙ u = C - A, pričom pre bod C platí: 1. |AC| = |r| . |AB|, 2. Ak r ≥ 0, tak bod C leží na polpriamke AB a ak r < 0, tak bod C leží na polpriamke opačnej k polpriamke AB (
obr. 1L8
).Násobok nulového vektora číslom r resp. nulový násobok vektora je nulový vektor, t. j. r 0 = 0, resp. 0u = 0. |
Násobenie vektora reálnym číslom je binárna relácia R x V → V, ktorá dvojici vektorov (r, v) ∈ R x V priradí práve jeden vektor w = r
v ∈ V spôsobom podľa predchádzajúcej definície. Geometrický význam tejto operácie je zrejmý: ide o rovnoľahlosť na priamke so stredom v bode A a koeficientom r.
Definícia je korektná, lebo vektor k u nezávisí od voľby umiestnenia vektora u.
Presvedčte sa o tom.
Osobitnou operáciou s vektormi je ich lineárna kombinácia ako zovšeobecnenie operácie násobenia vektora reálnym číslom a operácie sčitovania vektorov.
Definícia je korektná, lebo vektor k u nezávisí od voľby umiestnenia vektora u.
Presvedčte sa o tom.Osobitnou operáciou s vektormi je ich lineárna kombinácia ako zovšeobecnenie operácie násobenia vektora reálnym číslom a operácie sčitovania vektorov.
| Definícia 1L5. Nech je daných k vektorov v 1, v 2, …, v n . Každý vektor v vyjadrený v tvare v = c 1 v 1 + c 2 v 2 + … + c k v n , kde c 1, c 2, …, c n sú reálne čísla, sa nazýva lineárnou kombináciou vektorov v 1, v 2, …, v n . |
Poznámka 1L5.
Lineárna kombinácia vektorov je vektor.