Výpočet uhla dvoch nadrovín
Praktický návod na výpočet uhla dvoch rovín, ak poznáme ich normálové vektory, je uvedený v nasledujúcej vete:
| Veta 9L8. Nech α, β sú dve nadroviny priestoru E n . Potom uhol φ nadrovín α, β sa rovná uhlu φ dvoch priamok a, b takých, že a | α a b | β. |
Uhol dvoch nadrovín daných všeobecnými rovnicami sa vypočíta podľa tejto vety:
|
Veta 9L9. Nech α: a
1
x
1 + a
2
x
2 + … + a
n
x
n
+ a
0 = 0, β: b
1
x
1 + b
2
x
2 + … + b
n
x
n
+ b
0 = 0 sú dve nadroviny priestoru E
n
dané všeobecnými rovnicami. Potom pre uhol φ = ∠αβ, φ ∈ <0, π/2> nadrovín α, β platí: cos ∠αβ= 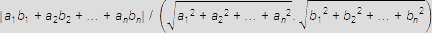
|
Priamo z vety 9L9 vyplýva nasledujúci dôsledok:
| Pre uhol φ nadrovín α: n.(X - P) = 0 a β: m.(X - Q) = 0 platí: cosφ = cos ∠αβ = |n.m| / (|n|.|m|). |