Základné vlastnosti uhla priamky s nadrovinou
Uhol priamky danej parametricky s nadrovinou danej všeobecnou rovnicou vypočítame podľa vzorca v nasledujúcej vete.
|
Veta 9L6. Nech p = P + <b>, kde b = (b
1, b
2, …, b
n
) a α: a
1
x
1 + a
2
x
2 + … + a
n
x
n
+ a
0 = 0. Potom pre uhol φ = ∠pα, φ ∈ <0, π/2> priamky p s nadrovinou α v priestore E
n
platí: sin ∠pα = 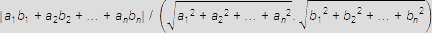 .
. |
V nasledujúcom dôsledku vety 9L6 je vzťah prepísaný vo vektorovom tvare:
| Pre uhol φ priamky p = A + <a> s nadrovinou α: n . (X - P) = 0 platí: sin φ = sin ∠pα = |an| / (|a|.|n|). |
Základné vlastnosti uhla priamky s nadrovinou vyjadruje nasledujúca veta:
|
Veta 9L7. Nech p je priamka, α nadrovina v euklidovskom priestore E
n
. Potom: a) ∠pα priamky p s nadrovinou α je číslo φ ∈ <0, π/2>, b) ∠pα = 0 ⇔ p || α, c) ∠pα = π/2 ⇔ p | α. |