Kolmý priemet priamky do lineárneho podpriestoru
|
Definícia 9L1. Nech M je ľubovoľná neprázdna množina bodov a α je lineárny podpriestor priestoru E
n
. Množina M* =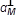 
∩ α = {X1 = X* =
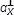∩ α ; X ∈ M}, kde
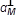= {α | X; X ∈ M} je kolmo premietací útvar množiny M a
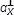α | X je kolmo premietací lineárny podpriestor bodu X, sa nazýva kolmý (ortogonálny) priemet množiny M do LP α. |
Poznámka 9L1.
Symbolický zápis: Kolmé priemety ľubovoľnej množiny (ľubovoľného lineárneho podpriestoru) M do iného lineárneho podpriestoru α budeme označovať aj dolným indexom 1, teda napr. M1 namiesto doterajšieho M* a keď nepríde k nedorozumeniu, uprednostníme nové označenie M1.