Odvodenie vzorca na výpočet obsahu kruhu s polomerom r
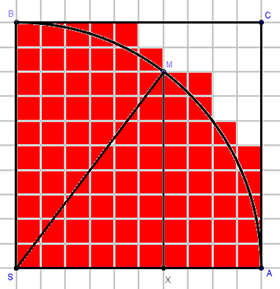
Z dôvodu zjednodušenia zisťovania obsahu kruhu s polomerom r, môžeme uvažovať o štvrťkruhu s uvedeným polomerom, a teda platí:
|J| < 1/4 S < |O|, z čoho
4.|J| < S < 4.|O|.
Štvorec SACB (pozri obrázok) je pri zvolenej štvorcovej sieti pre n = 10 zložený zo 100 štvorcov. Keďže strana štvorčeka je 1/10.r, tak obsah jedného malého štvorca je 0,01.r2. Obsah znázorneného jadra J1 má 69 štvorcov, teda |J1| = 0,69 r2. Obsah znázorneného obalu má 69 + 17 = 86 štvorcov, teda |O1| = 0,86 r2.
4.|J| < S < 4.|O|
4.0,69 r2 < S < 4.0,86 r2
2,76 r2 < S < 3,44 r2
Po zjemnení štvorcovej siete pre n = 100 je štvorec SACB zložený z 10 000 štvorcov. Obsah jedného z nich je |J2| = 0,0001 r2 (lebo strana je 1/100 r). Potom 4.(počet štvorcov jadra).0,0001 r2 < S < 4.(počet štvorcov obalu). 0,0001 r2
3,1409 r2 < S < 3,1420 r2.
Obsah kruhu sme ohraničili číslami 3,1409 a 3,1420. Tieto čísla sú blízko čísla π, ktoré nazývame Ludolfovým číslom a určili sme ho s presnosťou na dve desatinné miesta 3, 14. Obsah kruhu S = πr2.
Číslo π je iracionálnym číslom.
|J| < 1/4 S < |O|, z čoho
4.|J| < S < 4.|O|.
Štvorec SACB (pozri obrázok) je pri zvolenej štvorcovej sieti pre n = 10 zložený zo 100 štvorcov. Keďže strana štvorčeka je 1/10.r, tak obsah jedného malého štvorca je 0,01.r2. Obsah znázorneného jadra J1 má 69 štvorcov, teda |J1| = 0,69 r2. Obsah znázorneného obalu má 69 + 17 = 86 štvorcov, teda |O1| = 0,86 r2.
4.|J| < S < 4.|O|
4.0,69 r2 < S < 4.0,86 r2
2,76 r2 < S < 3,44 r2
Po zjemnení štvorcovej siete pre n = 100 je štvorec SACB zložený z 10 000 štvorcov. Obsah jedného z nich je |J2| = 0,0001 r2 (lebo strana je 1/100 r). Potom 4.(počet štvorcov jadra).0,0001 r2 < S < 4.(počet štvorcov obalu). 0,0001 r2
3,1409 r2 < S < 3,1420 r2.
Obsah kruhu sme ohraničili číslami 3,1409 a 3,1420. Tieto čísla sú blízko čísla π, ktoré nazývame Ludolfovým číslom a určili sme ho s presnosťou na dve desatinné miesta 3, 14. Obsah kruhu S = πr2.
Číslo π je iracionálnym číslom.