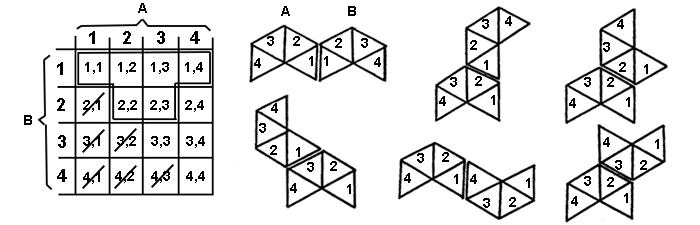
Po niekoľkých náhodných pokusoch napríklad s „rozstrihávaním modelu“ pravidelného osemstena sa dá vypozorovať, že vznikajúce siete môžeme chápať ako vhodné umiestnenia dvojice zhodných objektov A, B (pozri obrázok). Číslovanie hrán (1, 2, 3, 4) umožňuje prehľadnejšie zapisovať metódu ďalšieho získavania ďalších tvarov sietí. Všetky teoretické možnosti umiestnenia objektov A, B obsahuje tabuľka. V nej sme už pri zostavovaní vynechali dvojice patriace „pod hlavnú diagonálu“, pretože je zrejmá napríklad zhodnosť sietí (1,4) a (4,1) atď.

Po získaní šiestich rôznych tvarov sietí (pozri obrázok) vyplývajúcich z rôzneho usporiadania objektov A a B vzniká otázka, či sú týmto vyčerpané všetky možnosti, a teda koľko rôznych tvarov sietí má daný pravidelný osemsten. Podobne ako pri určovaní počtu rôznych tvarov sietí kocky, aj v tomto cvičení odpozorujeme možnosť „pohybu“ modelov stien, ktoré nepatria rovnobežníku, resp. lichobežníku určujúcemu dĺžku siete (je to maximálny počet trojuholníkov siete usporiadaných v páse). Takto je možné s prehľadom zistiť všetky možnosti zodpovedajúce podmienkam pre sieť pravidelného osemstena a môžeme ich taktiež usporiadať do príslušného .