Určovanie miery zložitejších rovinných útvarov
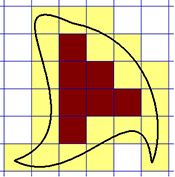
Jadro a obal útvaru sú zložené z konečného počtu štvorcov, preto ich obsahy môžeme vypočítať. Z definície jadra a obalu je zrejmé: J ⊂ U ⊂ O, a preto obsah útvaru môžeme ohraničiť: S(J) ≤ S(U) ≤ S(O).
Zjemňovaním štvorcovej siete vieme určiť mieru geometrického útvaru presnejšie: S(J´) ≤ S(U) ≤ S(O´) , kde J´ a O´ sú jadro a obal útvaru v zjemnenej štvorcovej sieti.
Ak takto postupujeme ďalej, môžeme za obsah útvaru považovať suprémum z hodnôt jadier daného útvaru a infímum z hodnôt obalov útvaru, t. j.
sup S(J) = S(U) = inf S(O).
Zjemňovaním štvorcovej siete vieme určiť mieru geometrického útvaru presnejšie: S(J´) ≤ S(U) ≤ S(O´) , kde J´ a O´ sú jadro a obal útvaru v zjemnenej štvorcovej sieti.
Ak takto postupujeme ďalej, môžeme za obsah útvaru považovať suprémum z hodnôt jadier daného útvaru a infímum z hodnôt obalov útvaru, t. j.
sup S(J) = S(U) = inf S(O).
|
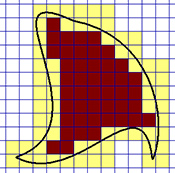
Jadro útvaru tvorí počet červených štvorcov vpísaných do útvaru (7 štvorcov). Obal útvaru tvorí počet žltých aj červených štvorcov, ktorými je útvar pokrytý (27 štvorcov). Obsah útvaru je teda ohraničený 7 ≤ S(U) ≤ 27 Po zjemnení zo štvorcovej siete so stranou štvorca 5 jednotiek na štvorec s polovičnou stranou získame ohraničenie: 45 ≤ S(U) ≤ 108 |
|
Poznámka:
Jadro a obal sa určuje aj pri miere úsečky a miere uhla.
Jadro a obal sa určuje aj pri miere úsečky a miere uhla.