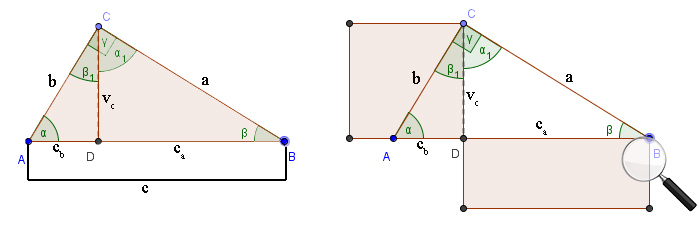
Euklidova veta o výške
Výška pravouhlého trojuholníka na preponu delí daný trojuholník na dva pravouhlé trojuholníky, ktoré sú obidva podobné danému trojuholníku a aj samy sebe. V pravouhlom trojuholníku ABC s pravým uhlom pri vrchole C označíme výšku na preponu vc. Päta výšky vc rozdelí preponu na dva úseky, ktoré označíme ca a cb.
Z podobnosti trojuholníkov ADC a CDB vyplýva: vc : cb = ca : vc. Po úprave dostaneme vzťah vc 2 = ca . cb. Uvedený vzťah je symbolickým zápisom Euklidovej vety o výške.
Z podobnosti trojuholníkov ADC a CDB vyplýva: vc : cb = ca : vc. Po úprave dostaneme vzťah vc 2 = ca . cb. Uvedený vzťah je symbolickým zápisom Euklidovej vety o výške.
|
Euklidova veta o výške:
Obsah štvorca zostrojeného nad výškou pravouhlého trojuholníka sa rovná obsahu obdĺžnika zostrojeného z oboch úsekov prepony. |