Injektívne zobrazenie – príklad
Zadanie:
Dané sú množiny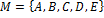 a
a
 a zobrazenia
a zobrazenia
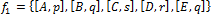 ,
,
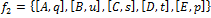 ,
,
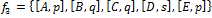 ,
,
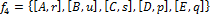 , z množiny
, z množiny
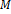 do množiny
do množiny
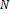 . Určíme, ktoré zo zobrazení sú injektívne (prosté).
. Určíme, ktoré zo zobrazení sú injektívne (prosté).
Riešenie:
V zobrazení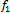 si všimnime usporiadané dvojice
si všimnime usporiadané dvojice
 . Prvky na prvých miestach sú rôzne, ale na druhých miestach je v oboch usporiadaných dvojiciach prvok
. Prvky na prvých miestach sú rôzne, ale na druhých miestach je v oboch usporiadaných dvojiciach prvok
 . Platí teda:
. Platí teda:
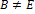 , ale
, ale
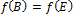 . Preto zobrazenie
. Preto zobrazenie
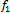 nie je injektívne (prosté).
nie je injektívne (prosté).
Dané sú množiny
Riešenie:
V zobrazení
Jednoduchšie vysvetlenie:
|
|
|
|
|
Zadanie:
Dané sú množiny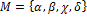 a
a
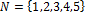 a zobrazenie
a zobrazenie
 z množiny
z množiny
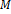 do množiny
do množiny
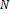 vrcholovým grafom. Určíme, či zobrazenie
vrcholovým grafom. Určíme, či zobrazenie
 je injektívne.
je injektívne.
Riešenie:
Pretože do žiadneho prvku množiny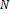 nesmeruje viac ako jedna šípka, zobrazenie
nesmeruje viac ako jedna šípka, zobrazenie
 je injektívne.
je injektívne.
Dané sú množiny
Riešenie:
Pretože do žiadneho prvku množiny