Dôkaz matematickou indukciou – riešenie úloh
Zadanie:
Dokážte, že pre súčet prvých n nepárnych čísel platí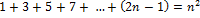 .
.
Riešenie:
Použijeme dôkaz matematickou indukciou.
Dokážte, že pre súčet prvých n nepárnych čísel platí
Riešenie:
Použijeme dôkaz matematickou indukciou.
|
|||
|
|||
|
Zadanie:
Dokážte, že pre súčet prvých n prirodzených čísel platí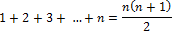 .
.
Riešenie:
Použijeme dôkaz matematickou indukciou.
Dokážte, že pre súčet prvých n prirodzených čísel platí
Riešenie:
Použijeme dôkaz matematickou indukciou.
|
|||
|
|||
|
Zadanie:
Dokážte, že pre každé prirodzené číslo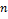 platí
platí
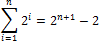 .
.
Riešenie:
Najprv si uvedomíme, že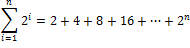 .
.
Teraz použijeme dôkaz matematickou indukciou.
Dokážte, že pre každé prirodzené číslo
Riešenie:
Najprv si uvedomíme, že
Teraz použijeme dôkaz matematickou indukciou.
|
|||
|
|||
|
Zadanie:
Dokážte, že pre každé prirodzené číslo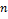 väčšie ako
väčšie ako
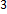 platí
platí
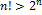 .
.
Riešenie:
Najprv si pripomenieme, že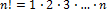 .
.
Teraz použijeme dôkaz matematickou indukciou.
Dokážte, že pre každé prirodzené číslo
Riešenie:
Najprv si pripomenieme, že
Teraz použijeme dôkaz matematickou indukciou.
|
|||
|
|||
|