Bijektívne zobrazenie
Ako teda zistíme, či je zobrazenie f bijektívne?
Predpokladajme, že zobrazenie
 z množiny
z množiny
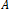 do množiny
do množiny
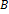 je určené vymenovaním usporiadaných dvojíc.
je určené vymenovaním usporiadaných dvojíc.
|
|
|
|
|
Teraz predpokladajme, že zobrazenie
 z množiny
z množiny
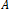 do množiny
do množiny
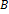 je určené vrcholovým grafom.
je určené vrcholovým grafom.
|
|
|
|
|
Všimnite si, že pri bijektívnom zobrazení možno prvky navzájom „popáriť“. To znamená, že každému prvku množiny
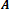 zodpovedá práve jeden prvok množiny
zodpovedá práve jeden prvok množiny
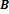 a naopak.
a naopak.