Tranzitívna binárna relácia
Ako sme už uviedli v definícii, reláciu
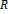 definovanú v množine
definovanú v množine
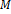 nazývame tranzitívnou, ak
nazývame tranzitívnou, ak
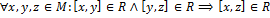 (čítame: ak pre každú trojicu prvkov
(čítame: ak pre každú trojicu prvkov
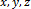 z množiny
z množiny
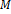 platí, že ak
platí, že ak
 je v relácii s
je v relácii s
 a
a
 je v relácii so
je v relácii so
 , potom
, potom
 je v relácii so
je v relácii so
 ).
).
Vysvetlime si teraz túto definíciu na príklade.
|
Teraz si všimneme, ako sa tranzitívnosť relácie prejavuje na jej vrcholovom grafe.
Vo vrcholovom grafe tranzitívnej relácie nenájdeme:
|
|
|