Antireflexívna binárna relácia
Ako sme už uviedli v definícii, reláciu
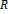 definovanú v množine
definovanú v množine
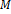 nazývame antireflexívnou, ak
nazývame antireflexívnou, ak
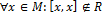 (čítame: ak pre každý prvok
(čítame: ak pre každý prvok
 z množiny
z množiny
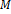 platí, že
platí, že
 nie je v relácii s
nie je v relácii s
 , teda sám so sebou).
, teda sám so sebou).
Vysvetlime si teraz túto definíciu na príklade.
|