Dedekindova teória
Ďalšiu veľmi známu teóriu reálnych čísel vybudoval nemecký matematik Julius Wilhelm Richard Dedekind. Je založená na špeciálnych množinách racionálnych čísel, ktoré sú nám bližšie ako fundamentálne postupnosti, a preto si o nej povieme trochu viac.
Veľmi dôležitým pojmom v Dedekindovej teórii je rez množiny racionálnych čísel. Je to taká podmnožina množiny racionálnych čísel, ktorá:
|
|||
|
|||
|
|||
|
Každý rez množiny racionálnych čísel predstavuje potom reálne číslo. Napríklad reálne číslo √2 predstavuje zjednotenie množiny záporných racionálnych čísel s množinou tých nezáporných racionálnych čísel, ktorých druhá mocnina je menšia ako 2. Reálne číslo √3 predstavuje zjednotenie množiny záporných racionálnych čísel s množinou tých nezáporných racionálnych čísel, ktorých druhá mocnina je menšia ako 3. Reálne číslo
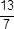 predstavuje množina tých racionálnych čísel, ktoré sú menšie ako
predstavuje množina tých racionálnych čísel, ktoré sú menšie ako
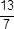 , reálne číslo π predstavuje množina tých racionálnych čísel, ktoré sú menšie ako π. Na množine všetkých rezov racionálnych čísel definujeme operácie sčítania a násobenia a reláciu usporiadania.
, reálne číslo π predstavuje množina tých racionálnych čísel, ktoré sú menšie ako π. Na množine všetkých rezov racionálnych čísel definujeme operácie sčítania a násobenia a reláciu usporiadania.
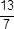 predstavuje množina tých racionálnych čísel, ktoré sú menšie ako
predstavuje množina tých racionálnych čísel, ktoré sú menšie ako
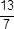 , reálne číslo π predstavuje množina tých racionálnych čísel, ktoré sú menšie ako π. Na množine všetkých rezov racionálnych čísel definujeme operácie sčítania a násobenia a reláciu usporiadania.
, reálne číslo π predstavuje množina tých racionálnych čísel, ktoré sú menšie ako π. Na množine všetkých rezov racionálnych čísel definujeme operácie sčítania a násobenia a reláciu usporiadania.