Iracionálnosť čísla odmocnina z dvoch
S riešením diofantovských rovníc súvisí napríklad aj problém, či číslo √2 je racionálne. Ak by bolo, potom by existovali také prirodzené čísla p a q, že
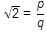 . Umocnením obidvoch strán rovnice dostaneme
. Umocnením obidvoch strán rovnice dostaneme
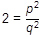 a následnou úpravou získame diofantovskú rovnicu 2q
2 = p
2. Nie je ťažké dokázať, že táto rovnica nemá riešenie, a teda že číslo √2 nie je racionálne.
a následnou úpravou získame diofantovskú rovnicu 2q
2 = p
2. Nie je ťažké dokázať, že táto rovnica nemá riešenie, a teda že číslo √2 nie je racionálne.
Pri dôkaze použijeme kanonický rozklad čísla. Prvočíslo 2 sa v kanonickom rozklade čísla q nachádza 0, 1, 2, 3, …-krát. Teda v kanonickom rozklade čísla q 2 sa nachádza párny počet ráz. Z toho vyplýva, že v kanonickom rozklade čísla 2q 2 sa nachádza nepárny počet ráz. Podobnou úvahou zistíme, že prvočíslo 2 sa v kanonickom rozklade čísla p 2 nachádza párny počet ráz.
Pretože kanonický rozklad čísla je určený jednoznačne, rovnica 2q 2 = p 2 nemá v obore prirodzených čísel riešenie, a teda číslo √2 nie je racionálne.
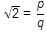 . Umocnením obidvoch strán rovnice dostaneme
. Umocnením obidvoch strán rovnice dostaneme
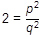 a následnou úpravou získame diofantovskú rovnicu 2q
2 = p
2. Nie je ťažké dokázať, že táto rovnica nemá riešenie, a teda že číslo √2 nie je racionálne.
a následnou úpravou získame diofantovskú rovnicu 2q
2 = p
2. Nie je ťažké dokázať, že táto rovnica nemá riešenie, a teda že číslo √2 nie je racionálne.Pri dôkaze použijeme kanonický rozklad čísla. Prvočíslo 2 sa v kanonickom rozklade čísla q nachádza 0, 1, 2, 3, …-krát. Teda v kanonickom rozklade čísla q 2 sa nachádza párny počet ráz. Z toho vyplýva, že v kanonickom rozklade čísla 2q 2 sa nachádza nepárny počet ráz. Podobnou úvahou zistíme, že prvočíslo 2 sa v kanonickom rozklade čísla p 2 nachádza párny počet ráz.
Pretože kanonický rozklad čísla je určený jednoznačne, rovnica 2q 2 = p 2 nemá v obore prirodzených čísel riešenie, a teda číslo √2 nie je racionálne.