Odmocniny
| Nech n je ľubovoľné prirodzené číslo, ktoré nie je druhou mocninou iného prirodzeného čísla. Potom číslo √ n nie je racionálne. |
Táto veta nám hovorí, že čísla √2, √3, √5, √6, √7, √8, √10, √11 nie sú racionálne.
Nech n je ľubovoľné prirodzené číslo, ktoré nie je treťou mocninou iného prirodzeného čísla. Potom číslo
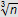nie je racionálne.
|
Táto veta nám hovorí, že čísla
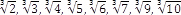nie sú racionálne.
S číslami, ktoré nie sú racionálne, sa stretávame aj pri riešení kvadratických rovníc. Vyriešme tri z nich:
nie sú racionálne.S číslami, ktoré nie sú racionálne, sa stretávame aj pri riešení kvadratických rovníc. Vyriešme tri z nich:
| x 2 - 3x - 7 = 0 | x 2 - 6x + 7 = 0 | x 2 + 3x + 1 = 0 |
| D = (-3)2 - 4 ∙ 1 ∙ (-7) = 37 | D = (-6)2 - 4 ∙ 1 ∙ 7 = 8 | D = 32 - 4 ∙ 1 ∙ 1 = 5 |
|
|
|
|
|
|
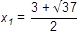
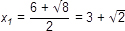
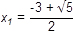
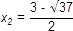
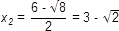
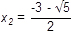
Ani jedno riešenie týchto troch rovníc nie je racionálne. V množine racionálnych čísel teda rovnice riešenie nemajú, ale v množine reálnych čísel má každá z nich dve riešenia.