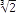Algebrické čísla – definícia a príklady
Ak by sme si zvolili ľubovoľnú rovnicu typu a
n
x
n
+ a
n
−1
x
n
−1 + a
n
−2
x
n
−2 + … + a
2
x
2 + a
1
x + a
0 = 0, za koeficienty
a n , a n −1, a n −2, …, a 2, a 1, a 0 by sme si zvolili ľubovoľné racionálne čísla a keby sme túto rovnicu vyriešili, dostali by sme jej korene. Tieto korene by boli algebrickými číslami.
Algebrické číslo je teda také číslo, ktoré je koreňom nejakej rovnice typu
a n x n + a n −1 x n −1 + a n −2 x n −2 + … + a 2 x 2 + a 1 x + a 0 = 0, kde a n , a n −1, a n −2, …, a 2, a 1, a 0 sú racionálne čísla.
a n , a n −1, a n −2, …, a 2, a 1, a 0 by sme si zvolili ľubovoľné racionálne čísla a keby sme túto rovnicu vyriešili, dostali by sme jej korene. Tieto korene by boli algebrickými číslami.
Algebrické číslo je teda také číslo, ktoré je koreňom nejakej rovnice typu
a n x n + a n −1 x n −1 + a n −2 x n −2 + … + a 2 x 2 + a 1 x + a 0 = 0, kde a n , a n −1, a n −2, …, a 2, a 1, a 0 sú racionálne čísla.
Algebrické čísla sú napríklad:
|
|
|
|
|
|
|
Existujú aj také reálne čísla, ktoré nie sú algebrické. Takéto čísla nazývame transcendentné. Sú to napríklad π, e (Eulerovo číslo), sin 10°, cos 10°, tg 10°, cotg 10°.
Dá sa dokázať, že súčtom, súčinom, rozdielom a aj podielom algebrických čísel sú algebrické čísla. Dá sa dokonca dokázať, že množina algebrických čísel spolu s operáciami sčítania a násobenia tvorí pole, ale to presahuje rámec týchto učebných textov.
Dá sa dokázať, že súčtom, súčinom, rozdielom a aj podielom algebrických čísel sú algebrické čísla. Dá sa dokonca dokázať, že množina algebrických čísel spolu s operáciami sčítania a násobenia tvorí pole, ale to presahuje rámec týchto učebných textov.