Iracionálne a algebrické čísla
Pojem iracionálneho čísla – úvod
Pojem iracionálne číslo si najprv podrobnejšie vysvetlíme.
Už na základnej škole sme sa stretli s Pytagorovou vetou. Podľa nej preponu c pravouhlého trojuholníka s odvesnami a, b vypočítame podľa vzorca c =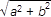 (možno je vám známejší vzorec c
2 = a
2 + b
2 ). Vezmime si pravouhlý trojuholník, ktorého obe odvesny majú dĺžku 1. Potom podľa tohto vzorca má jeho prepona dĺžku c =
(možno je vám známejší vzorec c
2 = a
2 + b
2 ). Vezmime si pravouhlý trojuholník, ktorého obe odvesny majú dĺžku 1. Potom podľa tohto vzorca má jeho prepona dĺžku c =
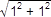 = √1 + 1 = √2.
= √1 + 1 = √2.
Pokúsme sa vyjadriť číslo √2 v tvare zlomku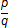 , p ∈ Z, q ∈ N, (p,q) = 1 (posledný výraz znamená, že čísla p a q sú nesúdeliteľné, teda že ich najväčším spoločným deliteľom je číslo 1).
, p ∈ Z, q ∈ N, (p,q) = 1 (posledný výraz znamená, že čísla p a q sú nesúdeliteľné, teda že ich najväčším spoločným deliteľom je číslo 1).
Nech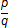 = √2. Potom
= √2. Potom
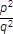 = 2, z čoho vyplýva, že p
2 = 2q
2.
= 2, z čoho vyplýva, že p
2 = 2q
2.
Urobme si rozklad čísla p na súčin prvočísel. Nech sa v ňom dvojka nachádza s exponentom k (k je nezáporné celé číslo). Potom v rozklade čísla p 2 na súčin prvočísel sa dvojka nachádza s exponentom 2k. Podobne si urobme rozklad čísla q na súčin prvočísel. Nech sa v ňom dvojka nachádza s exponentom l (l je nezáporné celé číslo). Potom v rozklade čísla q 2 na súčin prvočísel sa dvojka nachádza s exponentom 2l, a teda v rozklade čísla 2q 2 na súčin prvočísel sa dvojka nachádza s exponentom 2l + 1.
Vidíme, že v rozklade čísla p 2 na súčin prvočísel sa dvojka nachádza s párnym exponentom a v rozklade čísla 2q 2 na súčin prvočísel sa dvojka nachádza s nepárnym exponentom. Pretože vieme, že rozklad čísla na súčin prvočísel je jednoznačne určený, nemôže nastať rovnosť p 2 = 2q 2, z čoho vyplýva, že √2 sa nedá vyjadriť v tvare zlomku. Vidíme teda, že číslo √2 nie je racionálne. Podobne by sme vedeli ukázať, že racionálne nie sú ani čísla √3, √5, √6, √7, √8,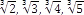 a mnohé ďalšie.
a mnohé ďalšie.
Už na základnej škole sme sa stretli s Pytagorovou vetou. Podľa nej preponu c pravouhlého trojuholníka s odvesnami a, b vypočítame podľa vzorca c =
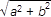 (možno je vám známejší vzorec c
2 = a
2 + b
2 ). Vezmime si pravouhlý trojuholník, ktorého obe odvesny majú dĺžku 1. Potom podľa tohto vzorca má jeho prepona dĺžku c =
(možno je vám známejší vzorec c
2 = a
2 + b
2 ). Vezmime si pravouhlý trojuholník, ktorého obe odvesny majú dĺžku 1. Potom podľa tohto vzorca má jeho prepona dĺžku c =
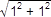 = √1 + 1 = √2.
= √1 + 1 = √2.Pokúsme sa vyjadriť číslo √2 v tvare zlomku
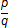 , p ∈ Z, q ∈ N, (p,q) = 1 (posledný výraz znamená, že čísla p a q sú nesúdeliteľné, teda že ich najväčším spoločným deliteľom je číslo 1).
, p ∈ Z, q ∈ N, (p,q) = 1 (posledný výraz znamená, že čísla p a q sú nesúdeliteľné, teda že ich najväčším spoločným deliteľom je číslo 1).Nech
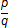 = √2. Potom
= √2. Potom
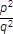 = 2, z čoho vyplýva, že p
2 = 2q
2.
= 2, z čoho vyplýva, že p
2 = 2q
2.Urobme si rozklad čísla p na súčin prvočísel. Nech sa v ňom dvojka nachádza s exponentom k (k je nezáporné celé číslo). Potom v rozklade čísla p 2 na súčin prvočísel sa dvojka nachádza s exponentom 2k. Podobne si urobme rozklad čísla q na súčin prvočísel. Nech sa v ňom dvojka nachádza s exponentom l (l je nezáporné celé číslo). Potom v rozklade čísla q 2 na súčin prvočísel sa dvojka nachádza s exponentom 2l, a teda v rozklade čísla 2q 2 na súčin prvočísel sa dvojka nachádza s exponentom 2l + 1.
Vidíme, že v rozklade čísla p 2 na súčin prvočísel sa dvojka nachádza s párnym exponentom a v rozklade čísla 2q 2 na súčin prvočísel sa dvojka nachádza s nepárnym exponentom. Pretože vieme, že rozklad čísla na súčin prvočísel je jednoznačne určený, nemôže nastať rovnosť p 2 = 2q 2, z čoho vyplýva, že √2 sa nedá vyjadriť v tvare zlomku. Vidíme teda, že číslo √2 nie je racionálne. Podobne by sme vedeli ukázať, že racionálne nie sú ani čísla √3, √5, √6, √7, √8,
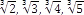 a mnohé ďalšie.
a mnohé ďalšie.