Poďme si tento proces zopakovať všeobecne. Zvoľme si komplexné číslo x + yi  a hľadajme také komplexné číslo a + bi, aby platilo x+yi=(a+bi) ² . Samozrejme a, b, x, y sú reálne čísla.



Podľa očakávania sme dostali kvadratickú rovnicu pre b ² . Príslušný diskriminat D sa rovná D=16x ² +16y ² = 16(x ² +y ² )

Vidíme, že je vždy nezáporný, preto má príslušná kvadratická rovnica vždy riešenie a to
 

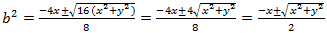
Z úloh na úvod ale vieme, že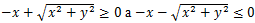 , pričom rovnosť nastane jedine pre x = y=0. To znamená, že nutne b²= 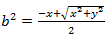 a teda 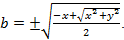 Keďže zo vzťahu a = 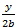  potom už a ľahko vypočítame.

Práve sme ukázali, že odmocnina z komplexného čísla vždy existuje a sú to vždy dve čísla líšiace sa znamienkom (okrem odmocniny z 0, ktorá je len jedna).