Ako ste sa presvedčili v predchádzajúcej úlohe, nie každá štvorcová matica má inverznú.

Teraz si ukážeme, ako sa dá inverzná matica vypočítať s pomocou riadkových ekvivalentných úprav.

Zadanie:
Ukážeme si to na matici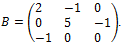

Riešenie:
Vytvoríme pomocnú maticu a to tak, k danej matici pripíšeme jednotkovú maticu:

.
Túto maticu budeme upravovať riadkovými elementárnymi úpravami tak, aby v ľavej polovici vznikla jednotková. Keď sa tak stane, v pravej polovici bude hľadaná inverzná matica.

Začneme tak, že prvý stĺpec upravíme tak, aby pod horným nenulovým číslom boli samé nuly. Na to stačí 3. riadok vynásobiť 2 a k nemu pričítať 1. riadok.


Teraz vyrobíme nuly v 2. stĺpci a to hore a dole. Predtým bude výhodné vymeniť 2. a 3. riadok.


Od 1. riadku odčítame 2. riadok a súčasne k 3. riadku pričítame 5-násobok 2. riadku.


Všetky nuly už máme „vyrobené“. Už ostáva len na hlavnej uhlopriečke dostať nuly. Preto 1. riadok vydelíme 2, 2. riadok a 3. riadok číslom -1.

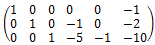
Vľavo sme dostali jednotkovú, tak vpravo musí byť inverzná: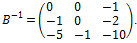 . Presvedčte sa o tom!