Definícia 8.14
A teraz prejdeme k všeobecnému násobeniu. Podobne ako nemôžeme sčitovať ľubovoľné matice, ani násobiť nemôžeme ľubovoľné matice. Pozor, je to ale inak ako pri sčítaní.
|
Definícia 8.14 Nech A je matica typu m × n a B matica typu n x r. Súčinom matíc A. B nazývame maticu C typu m x r, pre ktorej všetky prvky platí 
Všimnite si, že pri tomto násobení, musela mať matica A toľko stĺpcov ako matica B riadkov. To znamená, že na rozdiel od súčtu matíc, násobenie matíc nie je komutatívne. Vyplýva to už z toho, že napríklad A 2,5 .B 5,3 sa dá násobiť a B 5,3 .A 2,5 sa nedá násobiť. |
Najprv si násobenie ukážeme na konkrétnom príklade.
Nech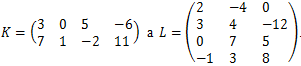
Vidíme, že prvá matica má 4 stĺpce a 2. matica 4 riadky. Preto môžeme násobiť K . L = M. Matica M bude typu 2 × 3 na počesť 2 riadkov matice K a 3 stĺpcov matice L.
Poďme vypočítať prvok napríklad m_2,1. Tento prvok dostaneme tak, že budeme násobiť 2. riadok prvej matice s 1. stĺpcom 2. matice. Teda ako keby sme násobili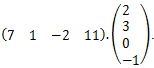
. Takže m
2,1
= 7.2 + 1.3 + (−2).0 + 11(−1) = 6.
Poďme ešte spolu vypočítať ešte prvok m_1,3. Tento prvok dostaneme tak, ako keby sme násobili 1. riadok prvej matice s 3. stĺpcom 2. matice. Teda ako keby sme násobili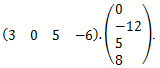
. Takže m
1,3
= 3.0 + 0.(-12) + 5.5 + (-6).8 = -23.
Takže už máme K.L =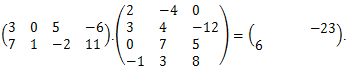
Nech
Vidíme, že prvá matica má 4 stĺpce a 2. matica 4 riadky. Preto môžeme násobiť K . L = M. Matica M bude typu 2 × 3 na počesť 2 riadkov matice K a 3 stĺpcov matice L.Poďme vypočítať prvok napríklad m_2,1. Tento prvok dostaneme tak, že budeme násobiť 2. riadok prvej matice s 1. stĺpcom 2. matice. Teda ako keby sme násobili
. Takže m
2,1
= 7.2 + 1.3 + (−2).0 + 11(−1) = 6.Poďme ešte spolu vypočítať ešte prvok m_1,3. Tento prvok dostaneme tak, ako keby sme násobili 1. riadok prvej matice s 3. stĺpcom 2. matice. Teda ako keby sme násobili
. Takže m
1,3
= 3.0 + 0.(-12) + 5.5 + (-6).8 = -23.Takže už máme K.L =